Chapitre 7 - Suites arithmétiques et géométriques
|
|
ISuites arithmétiques
1Généralités
Une suite de valeurs observée a une progression arithmétique si pour passer d'un terme au suivant, on lui ajoute une valeur fixée (la raison).
- La suite des nombre pair \( (P_n) = (0,2,4,6,8,10,...)\) a une progression arithmétique car elle augmente de \(2\) entre chaque terme.
- De même pour la suite des nombres impairs \( (I_n) = (1,3,5,7,9,11,...)\)
Une suite \((u_n)\) est arithmétique de raison \(r\) si elle est définie par la formule de récurrence : $$ \left\{ \begin{array}{ccc} u_{n+1} &=& u_{n} + r \\ u_0 &=& \text{terme initial} \end{array} \right. $$ 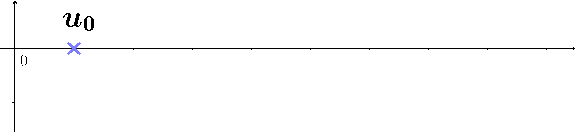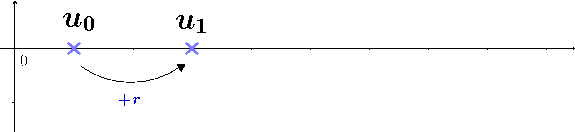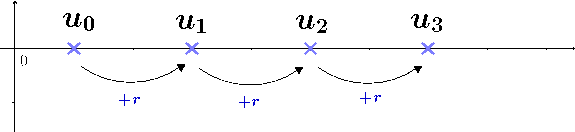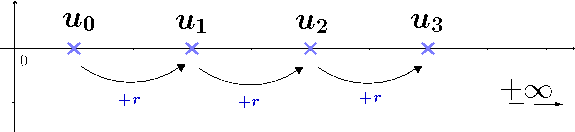
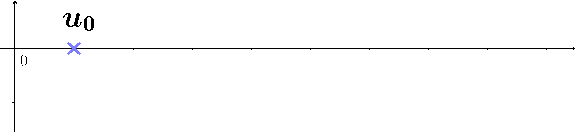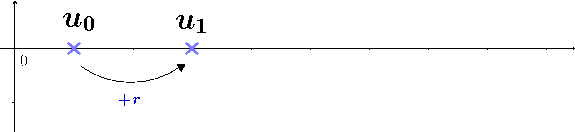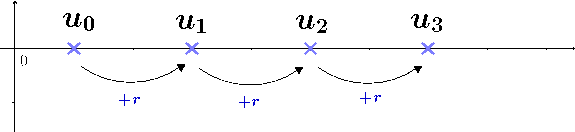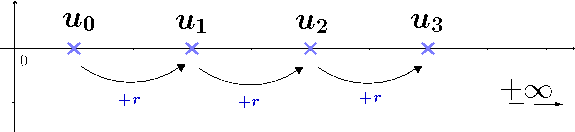

La formule récursive permet de calculer les termes dans l'ordre à partir du premier. La propriété suivante donne une formule explicite permettant le calcul de termes arbitraires :
Soit \((u_n)\) une suite arithmétique de raison \(r\) et de terme initial \(u_0\). Pour tout entier \(n\), on a : $$ u_n = u_0 + n r $$

2Propriétés

3Somme de termes consécutifs
Soit \(n\) un entier naturel : $$ 1 + 2 + 3 + ... + n = \frac{n (n+1)}{2} $$
On peut aussi écrire la somme à l'aide de l'opérateur \(\sum\) : $$ 1+2+3+ ... + n = \sum_{i=1}^n i $$
IISuites géométriques
1Généralités
Une suite de valeurs observée a une progression géométrique si pour passer d'un terme au suivant, on multiplie par une valeur fixée (la raison).
La suite des puissances de \(2\) \( (P_n) = (0,2,4,8,16,32,...)\) a une progression géométrique de raison \(2\). Cette suite n'est clairement pas arithmétique.
Une suite \((u_n)\) est géométrique de raison \(q\) si elle est définie par la formule de récurrence : $$ \left\{ \begin{array}{ccc} u_{n+1} &=& q imes u_{n} \\ u_0 &=& \text{terme initial} \end{array} \right. $$ 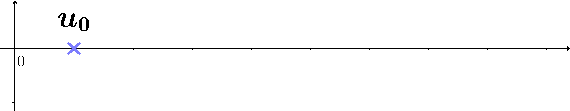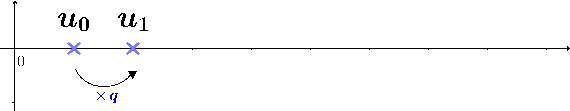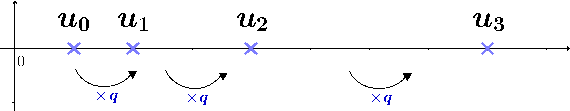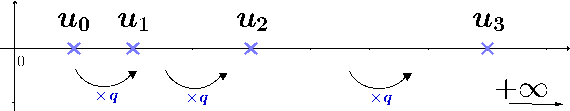
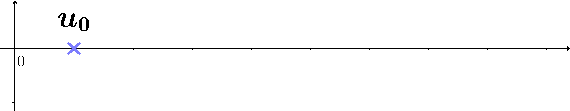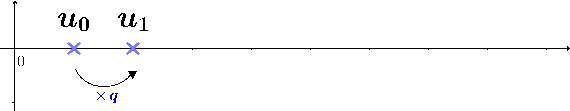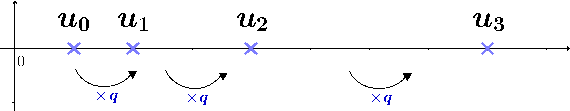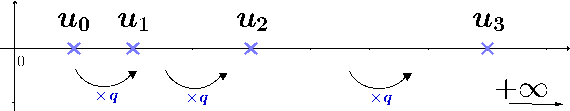

La formule récursive permet de calculer les termes dans l'ordre à partir du premier. La propriété suivante donne une formule explicite permettant le calcul de termes arbitraires :
Soit \((u_n)\) une suite géométrique de raison \(q\) et de terme initial \(u_0\). Pour tout entier \(n\), on a : $$ u_n = u_0 q^n $$

2Propriétés

3Somme de termes consécutifs
Soit \(n\) un entier naturel et \(q\) un nombre réel : $$ 1 + q + q^2 + ... + q^n = \frac{1 - q^{n+1}}{1 - q} $$
On peut aussi écrire la somme à l'aide de l'opérateur \(\sum\) : $$ 1 + q + q^2 + ... + q^n = \sum_{i=1}^n q^i $$
